
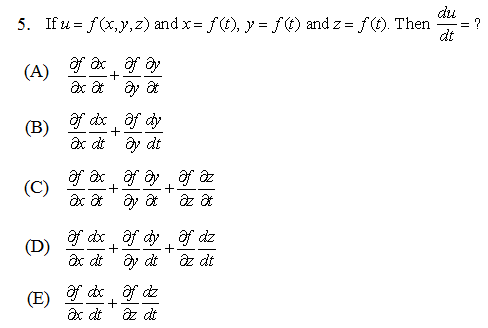
Likewise, 34% of students scored between 58 and 70. In the problem above, 34% of students scored between 70 and 82. Within 1 Standard Deviation Above the Mean= 34% Within 1 Standard Deviation Below the Mean= 34%īetween 1 and 2 Standard Deviations Above the Mean = 13.5% Between 1 and 2 Standard Deviations Below the Mean= 13.5%īetween 2 and 3 Standard Deviations Above the Mean = 2% Between 2 and 3 Standard Deviations Below the Mean= 2% To understand how standard deviation relates to the bell-curve take a look below: If the scores fell along a normal distribution and student X scored 95 points, then student X scored higher than approximately what percent of students?Īnswering this question correctly requires understanding standard distribution (that refers to the distribution of scores along the familiar bell-curve). To illustrate take a look at the following question.ġ- The standard deviation on a test was 12 points, and the mean was 70. You shouldn’t be so worried about how many statistics questions there are on the GRE, anyway. That is you will rely more on intuition than computation on statistics questions on the GRE.

The Statistics on the GRE is much simpler, and does not test your aptitude at crunching numbers as much as it does your ability to think about Statistics.
They run to their college stats textbooks, dust off the cover, roll up their sleeves, and start computing the standard deviations of a list of twenty, three-digit numbers. Many quake in their boots when they hear that there will be Statistics covered on the GRE. By Chris Lele on in GRE Data Analysis, GRE Math


 0 kommentar(er)
0 kommentar(er)
